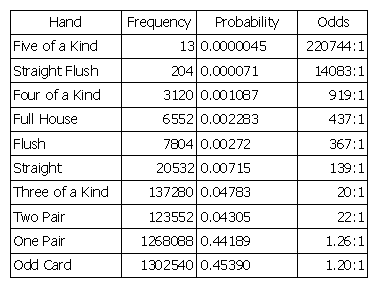
Texas Hold'em features 169 different starting hands. Despite this, there are only 9 categories of showdown hands available. In this poker hand ranking guide, we're going to introduce you to the worst showdown hands and make our way up to the best showdown hands. Poker Hand Rankings Quiz. Put your knowledge of poker hands to the test with the quiz below. Poker Starting Hands - Comprehensive guide to which poker hands you should play, including a 2020 Texas Hold'em poker starting hands chart.
- Texas Hold Em Starting Hands
- Good Hands In Texas Holdem
- Texas Holdem Poker Hand Ranking
- Texas Holdem Starting Hands
- Poker hands consist of the best five-card hand made up from any combination of the cards you are dealt and the community cards. Every beginning player, therefore, needs to understand the poker hand rankings to determine the strength of each player's hand and, subsequently, the winner. In this guide, we present the Texas Hold'em hands order.
- Trashy – Hands like Q5o, J6o, 52o and 84o are among the weakest starting hands in Texas Hold'em and should never be played as a raise first in. The majority of Texas Hold'em starting hands are in this category, so it's important to get into the habit of only selecting appropriate hands.
Introduction
The following table ranks the top hands in a 3-player game. This table assumes that all players stay in until the end.
Explanation of column headings:- Cards: Initial two-card hand.
- Probability of win: Probability that this hand will win, or tie for the win.
- Average win: This is how much the player will win on average, including his own bets, if the player does win. This is less than 3 because sometimes the player will have to split the pot.
- Expected value: This is how many units the player can expected to win (positive) or lose (negative) with this hand. For example if the player had a pair of aces and contibuted $1 to the pot then the player could expect to have a net win of $1.20.
- Probability: Probability of getting this hand to begin with.
- Additive probability: Probability of getting this hand or any stronger hand to begin with.
Initial Hold'em Hands in Rank Order for 3-Player Game
| Cards | Probability of Win | Average Win | Expected Value | Probability | Additive Probability |
| Pair of A's | 73.78% | 2.99 | 1.2034 | 0.45% | 0.45% |
| Pair of K's | 69.21% | 2.99 | 1.066 | 0.45% | 0.9% |
| Pair of Q's | 65.29% | 2.98 | 0.9475 | 0.45% | 1.36% |
| Pair of J's | 61.57% | 2.98 | 0.835 | 0.45% | 1.81% |
| Pair of T's | 58.02% | 2.98 | 0.7272 | 0.45% | 2.26% |
| Pair of 9's | 54.08% | 2.97 | 0.6084 | 0.45% | 2.71% |
| A/K suited | 51.77% | 2.94 | 0.5221 | 0.3% | 3.02% |
| Pair of 8's | 50.46% | 2.97 | 0.4986 | 0.45% | 3.47% |
| A/Q suited | 50.56% | 2.93 | 0.4824 | 0.3% | 3.77% |
| A/K unsuited | 49.28% | 2.93 | 0.4462 | 0.9% | 4.68% |
| A/J suited | 49.49% | 2.92 | 0.4461 | 0.3% | 4.98% |
| K/Q suited | 48.28% | 2.93 | 0.4128 | 0.3% | 5.28% |
| A/T suited | 48.5% | 2.91 | 0.4121 | 0.3% | 5.58% |
| A/Q unsuited | 48.01% | 2.93 | 0.4045 | 0.9% | 6.49% |
| Pair of 7's | 47.02% | 2.97 | 0.3945 | 0.45% | 6.94% |
| K/J suited | 47.22% | 2.92 | 0.3772 | 0.3% | 7.24% |
| A/J unsuited | 46.84% | 2.91 | 0.3652 | 0.9% | 8.14% |
| K/T suited | 46.24% | 2.91 | 0.3436 | 0.3% | 8.45% |
| A/9 suited | 46.16% | 2.9 | 0.3366 | 0.3% | 8.75% |
| K/Q unsuited | 45.61% | 2.92 | 0.3318 | 0.9% | 9.65% |
| A/T unsuited | 45.79% | 2.9 | 0.3289 | 0.9% | 10.56% |
| Q/J suited | 45.55% | 2.91 | 0.3256 | 0.3% | 10.86% |
| A/8 suited | 45.31% | 2.88 | 0.3058 | 0.3% | 11.16% |
| Pair of 6's | 43.77% | 2.96 | 0.2958 | 0.45% | 11.61% |
| Q/T suited | 44.59% | 2.9 | 0.2932 | 0.3% | 11.92% |
| K/J unsuited | 44.46% | 2.91 | 0.293 | 0.9% | 12.82% |
| A/7 suited | 44.32% | 2.87 | 0.2719 | 0.3% | 13.12% |
| K/9 suited | 43.88% | 2.89 | 0.2689 | 0.3% | 13.42% |
| J/T suited | 43.44% | 2.9 | 0.2582 | 0.3% | 13.73% |
| K/T unsuited | 43.42% | 2.9 | 0.2576 | 0.9% | 14.63% |
| A/9 unsuited | 43.25% | 2.88 | 0.2473 | 0.9% | 15.54% |
| A/5 suited | 43.59% | 2.85 | 0.2431 | 0.3% | 15.84% |
| Q/J unsuited | 42.76% | 2.9 | 0.2406 | 0.9% | 16.74% |
| A/6 suited | 43.19% | 2.86 | 0.2348 | 0.3% | 17.04% |
| Q/9 suited | 42.25% | 2.89 | 0.2193 | 0.3% | 17.35% |
| A/4 suited | 42.7% | 2.85 | 0.2161 | 0.3% | 17.65% |
| A/8 unsuited | 42.31% | 2.87 | 0.2136 | 0.9% | 18.55% |
| Q/T unsuited | 41.73% | 2.89 | 0.206 | 0.9% | 19.46% |
| K/8 suited | 41.91% | 2.88 | 0.2048 | 0.3% | 19.76% |
| Pair of 5's | 40.7% | 2.95 | 0.2017 | 0.45% | 20.21% |
| A/3 suited | 41.8% | 2.85 | 0.1901 | 0.3% | 20.51% |
| J/9 suited | 41.11% | 2.88 | 0.1844 | 0.3% | 20.81% |
| K/7 suited | 41.19% | 2.86 | 0.1786 | 0.3% | 21.12% |
| A/7 unsuited | 41.25% | 2.85 | 0.177 | 0.9% | 22.02% |
| K/9 unsuited | 40.88% | 2.88 | 0.1769 | 0.9% | 22.93% |
| J/T unsuited | 40.58% | 2.89 | 0.171 | 0.9% | 23.83% |
| A/2 suited | 40.86% | 2.85 | 0.163 | 0.3% | 24.13% |
| T/9 suited | 40.38% | 2.88 | 0.1617 | 0.3% | 24.43% |
| Q/8 suited | 40.28% | 2.87 | 0.1564 | 0.3% | 24.74% |
| K/6 suited | 40.29% | 2.85 | 0.1483 | 0.3% | 25.04% |
| A/5 unsuited | 40.46% | 2.83 | 0.1458 | 0.9% | 25.94% |
| A/6 unsuited | 40.04% | 2.84 | 0.1374 | 0.9% | 26.85% |
| Q/9 unsuited | 39.2% | 2.87 | 0.1262 | 0.9% | 27.75% |
| K/5 suited | 39.51% | 2.84 | 0.122 | 0.3% | 28.05% |
| J/8 suited | 39.14% | 2.87 | 0.1219 | 0.3% | 28.36% |
| A/4 unsuited | 39.45% | 2.83 | 0.1155 | 0.9% | 29.26% |
| K/8 unsuited | 38.75% | 2.86 | 0.1079 | 0.9% | 30.17% |
| Pair of 4's | 37.42% | 2.95 | 0.1026 | 0.45% | 30.62% |
| T/8 suited | 38.46% | 2.86 | 0.1004 | 0.3% | 30.92% |
| K/4 suited | 38.63% | 2.84 | 0.0956 | 0.3% | 31.22% |
| Q/7 suited | 38.33% | 2.85 | 0.0937 | 0.3% | 31.52% |
| J/9 unsuited | 38.05% | 2.87 | 0.0908 | 0.9% | 32.43% |
| A/3 unsuited | 38.5% | 2.83 | 0.0879 | 0.9% | 33.33% |
| K/7 unsuited | 37.96% | 2.84 | 0.0792 | 0.9% | 34.24% |
| 9/8 suited | 37.74% | 2.86 | 0.079 | 0.3% | 34.54% |
| Q/6 suited | 37.7% | 2.84 | 0.0712 | 0.3% | 34.84% |
| K/3 suited | 37.78% | 2.84 | 0.0712 | 0.3% | 35.14% |
| T/9 unsuited | 37.36% | 2.86 | 0.0692 | 0.9% | 36.05% |
| J/7 suited | 37.21% | 2.85 | 0.0605 | 0.3% | 36.35% |
| Q/8 unsuited | 37.09% | 2.85 | 0.0585 | 0.9% | 37.25% |
| A/2 unsuited | 37.47% | 2.82 | 0.0579 | 0.9% | 38.16% |
| K/6 unsuited | 37% | 2.83 | 0.0469 | 0.9% | 39.06% |
| K/2 suited | 36.91% | 2.83 | 0.0464 | 0.3% | 39.37% |
| Q/5 suited | 36.93% | 2.83 | 0.0455 | 0.3% | 39.67% |
| T/7 suited | 36.51% | 2.85 | 0.0394 | 0.3% | 39.97% |
| J/8 unsuited | 35.94% | 2.85 | 0.0237 | 0.9% | 40.87% |
| 9/7 suited | 35.95% | 2.84 | 0.0223 | 0.3% | 41.18% |
| Q/4 suited | 36.08% | 2.83 | 0.0203 | 0.3% | 41.48% |
| K/5 unsuited | 36.15% | 2.82 | 0.0183 | 0.9% | 42.38% |
| 8/7 suited | 35.65% | 2.84 | 0.0134 | 0.3% | 42.68% |
| Pair of 3's | 34.33% | 2.94 | 0.0087 | 0.45% | 43.14% |
| T/8 unsuited | 35.26% | 2.84 | 0.0026 | 0.9% | 44.04% |
| J/6 suited | 35.33% | 2.83 | 0.0009 | 0.3% | 44.34% |
| Q/3 suited | 35.22% | 2.83 | -0.0042 | 0.3% | 44.65% |
| Q/7 unsuited | 35.01% | 2.83 | -0.0082 | 0.9% | 45.55% |
| K/4 unsuited | 35.19% | 2.81 | -0.0104 | 0.9% | 46.46% |
| J/5 suited | 34.79% | 2.82 | -0.0182 | 0.3% | 46.76% |
| 9/8 unsuited | 34.55% | 2.84 | -0.0185 | 0.9% | 47.66% |
| T/6 suited | 34.64% | 2.83 | -0.0194 | 0.3% | 47.96% |
| Q/2 suited | 34.4% | 2.83 | -0.0279 | 0.3% | 48.27% |
| Q/6 unsuited | 34.33% | 2.82 | -0.0326 | 0.9% | 49.17% |
| 9/6 suited | 34.08% | 2.83 | -0.0357 | 0.3% | 49.47% |
| K/3 unsuited | 34.26% | 2.81 | -0.0374 | 0.9% | 50.38% |
| 8/6 suited | 33.88% | 2.83 | -0.0416 | 0.3% | 50.68% |
| J/7 unsuited | 33.86% | 2.83 | -0.0422 | 0.9% | 51.58% |
| 7/6 suited | 33.85% | 2.83 | -0.0424 | 0.3% | 51.89% |
| J/4 suited | 33.95% | 2.82 | -0.043 | 0.3% | 52.19% |
| Q/5 unsuited | 33.48% | 2.81 | -0.0607 | 0.9% | 53.09% |
| T/7 unsuited | 33.19% | 2.82 | -0.0626 | 0.9% | 54% |
| K/2 unsuited | 33.34% | 2.81 | -0.0642 | 0.9% | 54.9% |
| J/3 suited | 33.14% | 2.82 | -0.0659 | 0.3% | 55.2% |
| T/5 suited | 32.81% | 2.81 | -0.0768 | 0.3% | 55.51% |
| 9/7 unsuited | 32.6% | 2.82 | -0.0799 | 0.9% | 56.41% |
| Pair of 2's | 31.4% | 2.93 | -0.0804 | 0.45% | 56.86% |
| 8/7 unsuited | 32.33% | 2.82 | -0.0881 | 0.9% | 57.77% |
| Q/4 unsuited | 32.55% | 2.8 | -0.0886 | 0.9% | 58.67% |
| J/2 suited | 32.33% | 2.82 | -0.0891 | 0.3% | 58.97% |
| 6/5 suited | 32.21% | 2.82 | -0.0923 | 0.3% | 59.28% |
| 9/5 suited | 32.24% | 2.81 | -0.0927 | 0.3% | 59.58% |
| T/4 suited | 32.22% | 2.81 | -0.0945 | 0.3% | 59.88% |
| 7/5 suited | 32.1% | 2.82 | -0.0962 | 0.3% | 60.18% |
| 8/5 suited | 32.06% | 2.81 | -0.0979 | 0.3% | 60.48% |
| J/6 unsuited | 31.85% | 2.81 | -0.106 | 0.9% | 61.39% |
| Q/3 unsuited | 31.63% | 2.8 | -0.115 | 0.9% | 62.29% |
| T/3 suited | 31.42% | 2.81 | -0.1172 | 0.3% | 62.59% |
| T/6 unsuited | 31.16% | 2.8 | -0.1262 | 0.9% | 63.5% |
| J/5 unsuited | 31.26% | 2.79 | -0.1268 | 0.9% | 64.4% |
| 5/4 suited | 30.98% | 2.81 | -0.1295 | 0.3% | 64.71% |
| T/2 suited | 30.6% | 2.81 | -0.1405 | 0.3% | 65.01% |
| Q/2 unsuited | 30.72% | 2.8 | -0.1413 | 0.9% | 65.91% |
| 9/6 unsuited | 30.61% | 2.8 | -0.1421 | 0.9% | 66.82% |
| 6/4 suited | 30.42% | 2.81 | -0.1453 | 0.3% | 67.12% |
| 8/6 unsuited | 30.43% | 2.8 | -0.1473 | 0.9% | 68.02% |
| 7/6 unsuited | 30.41% | 2.8 | -0.1477 | 0.9% | 68.93% |
| 9/4 suited | 30.35% | 2.8 | -0.1492 | 0.3% | 69.23% |
| 7/4 suited | 30.21% | 2.81 | -0.1522 | 0.3% | 69.53% |
| J/4 unsuited | 30.35% | 2.79 | -0.1538 | 0.9% | 70.44% |
| 8/4 suited | 30.16% | 2.8 | -0.1542 | 0.3% | 70.74% |
| 9/3 suited | 29.78% | 2.8 | -0.1654 | 0.3% | 71.04% |
| J/3 unsuited | 29.44% | 2.79 | -0.1798 | 0.9% | 71.95% |
| 5/3 suited | 29.18% | 2.8 | -0.1821 | 0.3% | 72.25% |
| T/5 unsuited | 29.21% | 2.78 | -0.1872 | 0.9% | 73.15% |
| 9/2 suited | 28.98% | 2.8 | -0.1883 | 0.3% | 73.45% |
| 6/5 unsuited | 28.7% | 2.79 | -0.1998 | 0.9% | 74.36% |
| 6/3 suited | 28.55% | 2.8 | -0.2002 | 0.3% | 74.66% |
| 9/5 unsuited | 28.63% | 2.78 | -0.2035 | 0.9% | 75.57% |
| J/2 unsuited | 28.56% | 2.78 | -0.2052 | 0.9% | 76.47% |
| 7/5 unsuited | 28.54% | 2.78 | -0.2053 | 0.9% | 77.38% |
| T/4 unsuited | 28.55% | 2.78 | -0.2072 | 0.9% | 78.28% |
| 4/3 suited | 28.28% | 2.8 | -0.2074 | 0.3% | 78.58% |
| 8/5 unsuited | 28.47% | 2.78 | -0.2078 | 0.9% | 79.49% |
| 7/3 suited | 28.3% | 2.8 | -0.2082 | 0.3% | 79.79% |
| 8/3 suited | 28.28% | 2.8 | -0.2093 | 0.3% | 80.09% |
| 8/2 suited | 27.73% | 2.79 | -0.2253 | 0.3% | 80.39% |
| T/3 unsuited | 27.68% | 2.77 | -0.2324 | 0.9% | 81.3% |
| 5/2 suited | 27.3% | 2.79 | -0.2371 | 0.3% | 81.6% |
| 5/4 unsuited | 27.37% | 2.78 | -0.2401 | 0.9% | 82.5% |
| 6/2 suited | 26.65% | 2.79 | -0.2559 | 0.3% | 82.81% |
| 6/4 unsuited | 26.76% | 2.77 | -0.2576 | 0.9% | 83.71% |
| T/2 unsuited | 26.79% | 2.77 | -0.2578 | 0.9% | 84.62% |
| 4/2 suited | 26.49% | 2.79 | -0.2599 | 0.3% | 84.92% |
| 7/2 suited | 26.44% | 2.79 | -0.2628 | 0.3% | 85.22% |
| 9/4 unsuited | 26.59% | 2.77 | -0.2644 | 0.9% | 86.12% |
| 7/4 unsuited | 26.51% | 2.77 | -0.2657 | 0.9% | 87.03% |
| 8/4 unsuited | 26.42% | 2.77 | -0.2687 | 0.9% | 87.93% |
| 9/3 unsuited | 25.97% | 2.76 | -0.2825 | 0.9% | 88.84% |
| 3/2 suited | 25.61% | 2.79 | -0.285 | 0.3% | 89.14% |
| 5/3 unsuited | 25.46% | 2.76 | -0.2961 | 0.9% | 90.05% |
| 9/2 unsuited | 25.1% | 2.76 | -0.3073 | 0.9% | 90.95% |
| 6/3 unsuited | 24.74% | 2.76 | -0.3168 | 0.9% | 91.86% |
| 4/3 unsuited | 24.49% | 2.76 | -0.3238 | 0.9% | 92.76% |
| 7/3 unsuited | 24.47% | 2.76 | -0.3256 | 0.9% | 93.67% |
| 8/3 unsuited | 24.4% | 2.75 | -0.3285 | 0.9% | 94.57% |
| 8/2 unsuited | 23.79% | 2.75 | -0.3462 | 0.9% | 95.48% |
| 5/2 unsuited | 23.43% | 2.75 | -0.3558 | 0.9% | 96.38% |
| 6/2 unsuited | 22.69% | 2.75 | -0.3769 | 0.9% | 97.29% |
| 4/2 unsuited | 22.56% | 2.75 | -0.3801 | 0.9% | 98.19% |
| 7/2 unsuited | 22.44% | 2.74 | -0.3854 | 0.9% | 99.1% |
| 3/2 unsuited | 21.61% | 2.74 | -0.4072 | 0.9% | 100% |
| Total | 2.84 | 100% |
Methodology:
This table is the result of a random simulation of 68,612,544,000 games and assumes all players stay in until the end of the hand.
The following table shows my power rating for each initial 2-card hand in a 3-player game. The numbers are on a 0 to 40 scale. Use the top table if you have a pair, the middle table if your cards are suited, and the bottom table if your cards are unsuited. Except for a pair,look up your high card along the left and your low card along the top.
Inside Links
Texas Hold Em Starting Hands
In the poker game of Texas hold 'em, a starting hand consists of two hole cards, which belong solely to the player and remain hidden from the other players. Five community cards are also dealt into play. Betting begins before any of the community cards are exposed, and continues throughout the hand. The player's 'playing hand', which will be compared against that of each competing player, is the best 5-card poker hand available from his two hole cards and the five community cards. Unless otherwise specified, here the term hand applies to the player's two hole cards, or starting hand.
Essentials[edit]
There are 1326 distinct possible combinations of two hole cards from a standard 52-card deck in hold 'em, but since suits have no relative value in this poker variant, many of these hands are identical in value before the flop. For example, A♥J♥ and A♠J♠ are identical in value, because each is a hand consisting of an ace and a jack of the same suit.
Therefore, there are 169 non-equivalent starting hands in hold 'em, which is the sum total of : 13 pocket pairs, 13 × 12 / 2 = 78 suited hands and 78 unsuited hands (13 + 78 + 78 = 169).
These 169 hands are not equally likely. Hold 'em hands are sometimes classified as having one of three 'shapes':
- Pairs, (or 'pocket pairs'), which consist of two cards of the same rank (e.g. 9♠9♣). One hand in 17 will be a pair, each occurring with individual probability 1/221 (P(pair) = 3/51 = 1/17).

- Alternative means of making this calculation
- First Step
- As confirmed above.
- There are 1326 possible combination of opening hand.
- Second Step
- There are 6 different combos of each pair. 9h9c, 9h9s, 9h9d, 9c9s, 9c9d, 9d9s. Therefore, there are 78 possible combinations of pocket pairs (6 multiplied by 13 i.e. 22-AA)
- To calculate the odds of being dealt a pair
- 78 (the number of any particular pair being dealt. As above) divided by 1326 (possible opening hands)
- 78/1326 = 0.058 or 5.8%
- Suited hands, which contain two cards of the same suit (e.g. A♣6♣). 23.5% of all starting hands are suited.
Probability of first card is 1.0 (any of the 52 cards)Probability of second hand suit matching the first:There are 13 cards per suit, and one is in your hand leaving 12 remaining of the 51 cards remaining in the deck. 12/51=.2353 or 23.5%
- Offsuit hands, which contain two cards of a different suit and rank (e.g. K♠J♥). 70.6% of all hands are offsuit hands
Offsuit pairs = 78Other offsuit hands = 936
It is typical to abbreviate suited hands in hold 'em by affixing an 's' to the hand, as well as to abbreviate non-suited hands with an 'o' (for offsuit). That is,

- QQ represents any pair of queens,
- KQ represents any king and queen,
- AKo represents any ace and king of different suits, and
- JTs represents any jack and ten of the same suit.
Limit hand rankings[edit]
Some notable theorists and players have created systems to rank the value of starting hands in limit Texas hold'em. These rankings do not apply to no limit play.
Sklansky hand groups[edit]
:max_bytes(150000):strip_icc()/78432412-56a741f15f9b58b7d0e84d3a.jpg)
David Sklansky and Mason Malmuth[1] assigned in 1999 each hand to a group, and proposed all hands in the group could normally be played similarly. Stronger starting hands are identified by a lower number. Hands without a number are the weakest starting hands. As a general rule, books on Texas hold'em present hand strengths starting with the assumption of a nine or ten person table. The table below illustrates the concept:
Chen formula[edit]
The 'Chen Formula' is a way to compute the 'power ratings' of starting hands that was originally developed by Bill Chen.[2]
- Highest Card
- Based on the highest card, assign points as follows:
- Ace = 10 points, K = 8 points, Q = 7 points, J = 6 points.
- 10 through 2, half of face value (10 = 5 points, 9 = 4.5 points, etc.)
Good Hands In Texas Holdem
- Pairs
- For pairs, multiply the points by 2 (AA=20, KK=16, etc.), with a minimum of 5 points for any pair. 55 is given an extra point (i.e., 6).
- Suited
- Add 2 points for suited cards.
- Closeness
- Subtract 1 point for 1 gappers (AQ, J9)
- 2 points for 2 gappers (J8, AJ).
- 4 points for 3 gappers (J7, 73).
- 5 points for larger gappers, including A2 A3 A4
In the poker game of Texas hold 'em, a starting hand consists of two hole cards, which belong solely to the player and remain hidden from the other players. Five community cards are also dealt into play. Betting begins before any of the community cards are exposed, and continues throughout the hand. The player's 'playing hand', which will be compared against that of each competing player, is the best 5-card poker hand available from his two hole cards and the five community cards. Unless otherwise specified, here the term hand applies to the player's two hole cards, or starting hand.
Essentials[edit]
There are 1326 distinct possible combinations of two hole cards from a standard 52-card deck in hold 'em, but since suits have no relative value in this poker variant, many of these hands are identical in value before the flop. For example, A♥J♥ and A♠J♠ are identical in value, because each is a hand consisting of an ace and a jack of the same suit.
Therefore, there are 169 non-equivalent starting hands in hold 'em, which is the sum total of : 13 pocket pairs, 13 × 12 / 2 = 78 suited hands and 78 unsuited hands (13 + 78 + 78 = 169).
These 169 hands are not equally likely. Hold 'em hands are sometimes classified as having one of three 'shapes':
- Pairs, (or 'pocket pairs'), which consist of two cards of the same rank (e.g. 9♠9♣). One hand in 17 will be a pair, each occurring with individual probability 1/221 (P(pair) = 3/51 = 1/17).
- Alternative means of making this calculation
- First Step
- As confirmed above.
- There are 1326 possible combination of opening hand.
- Second Step
- There are 6 different combos of each pair. 9h9c, 9h9s, 9h9d, 9c9s, 9c9d, 9d9s. Therefore, there are 78 possible combinations of pocket pairs (6 multiplied by 13 i.e. 22-AA)
- To calculate the odds of being dealt a pair
- 78 (the number of any particular pair being dealt. As above) divided by 1326 (possible opening hands)
- 78/1326 = 0.058 or 5.8%
- Suited hands, which contain two cards of the same suit (e.g. A♣6♣). 23.5% of all starting hands are suited.
Probability of first card is 1.0 (any of the 52 cards)Probability of second hand suit matching the first:There are 13 cards per suit, and one is in your hand leaving 12 remaining of the 51 cards remaining in the deck. 12/51=.2353 or 23.5%
- Offsuit hands, which contain two cards of a different suit and rank (e.g. K♠J♥). 70.6% of all hands are offsuit hands
Offsuit pairs = 78Other offsuit hands = 936
It is typical to abbreviate suited hands in hold 'em by affixing an 's' to the hand, as well as to abbreviate non-suited hands with an 'o' (for offsuit). That is,
- QQ represents any pair of queens,
- KQ represents any king and queen,
- AKo represents any ace and king of different suits, and
- JTs represents any jack and ten of the same suit.
Limit hand rankings[edit]
Some notable theorists and players have created systems to rank the value of starting hands in limit Texas hold'em. These rankings do not apply to no limit play.
Sklansky hand groups[edit]
David Sklansky and Mason Malmuth[1] assigned in 1999 each hand to a group, and proposed all hands in the group could normally be played similarly. Stronger starting hands are identified by a lower number. Hands without a number are the weakest starting hands. As a general rule, books on Texas hold'em present hand strengths starting with the assumption of a nine or ten person table. The table below illustrates the concept:
Chen formula[edit]
The 'Chen Formula' is a way to compute the 'power ratings' of starting hands that was originally developed by Bill Chen.[2]
- Highest Card
- Based on the highest card, assign points as follows:
- Ace = 10 points, K = 8 points, Q = 7 points, J = 6 points.
- 10 through 2, half of face value (10 = 5 points, 9 = 4.5 points, etc.)
Good Hands In Texas Holdem
- Pairs
- For pairs, multiply the points by 2 (AA=20, KK=16, etc.), with a minimum of 5 points for any pair. 55 is given an extra point (i.e., 6).
- Suited
- Add 2 points for suited cards.
- Closeness
- Subtract 1 point for 1 gappers (AQ, J9)
- 2 points for 2 gappers (J8, AJ).
- 4 points for 3 gappers (J7, 73).
- 5 points for larger gappers, including A2 A3 A4
- Add an extra point if connected or 1-gap and your highest card is lower than Q (since you then can make all higher straights)
Phil Hellmuth's: 'Play Poker Like the Pros'[edit]
Phil Hellmuth's 'Play Poker Like the Pros' book published in 2003.
| Tier | Hands | Category |
|---|---|---|
| 1 | AA, KK, AKs, QQ, AK | Top 12 Hands |
| 2 | JJ, TT, 99 | |
| 3 | 88, 77, AQs, AQ | |
| 4 | 66, 55, 44, 33, 22, AJs, ATs, A9s, A8s | Majority Play Hands |
| 5 | A7s, A6s, A5s, A4s, A3s, A2s, KQs, KQ | |
| 6 | QJs, JTs, T9s, 98s, 87s, 76s, 65s | Suited Connectors |
Statistics based on real online play[edit]
Statistics based on real play with their associated actual value in real bets.[3]
| Tier | Hands | Expected Value |
|---|---|---|
| 1 | AA, KK, QQ, JJ, AKs | 2.32 - 0.78 |
| 2 | AQs, TT, AK, AJs, KQs, 99 | 0.59 - 0.38 |
| 3 | ATs, AQ, KJs, 88, KTs, QJs | 0.32 - 0.20 |
| 4 | A9s, AJ, QTs, KQ, 77, JTs | 0.19 - 0.15 |
| 5 | A8s, K9s, AT, A5s, A7s | 0.10 - 0.08 |
| 6 | KJ, 66, T9s, A4s, Q9s | 0.08 - 0.05 |
| 7 | J9s, QJ, A6s, 55, A3s, K8s, KT | 0.04 - 0.01 |
| 8 | 98s, T8s, K7s, A2s | 0.00 |
| 9 | 87s, QT, Q8s, 44, A9, J8s, 76s, JT | (-) 0.02 - 0.03 |
Nicknames for starting hands[edit]
In poker communities, it is common for hole cards to be given nicknames. While most combinations have a nickname, stronger handed nicknames are generally more recognized, the most notable probably being the 'Big Slick' - Ace and King of the same suit, although an Ace-King of any suit combination is less occasionally referred to as an Anna Kournikova, derived from the initials AK and because it 'looks really good but rarely wins.'[4][5] Hands can be named according to their shapes (e.g., paired aces look like 'rockets', paired jacks look like 'fish hooks'); a historic event (e.g., A's and 8's - dead man's hand, representing the hand held by Wild Bill Hickok when he was fatally shot in the back by Jack McCall in 1876); many other reasons like animal names, alliteration and rhyming are also used in nicknames.
Notes[edit]
Texas Holdem Poker Hand Ranking
- ^David Sklansky and Mason Malmuth (1999). Hold 'em Poker for Advanced Players. Two Plus Two Publications. ISBN1-880685-22-1
- ^Hold'em Excellence: From Beginner to Winner by Lou Krieger, Chapter 5, pages 39 - 43, Second Edition
- ^http://www.pokerroom.com/poker/poker-school/ev-stats/total-stats-by-card/[dead link]
- ^Aspden, Peter (2007-05-19). 'FT Weekend Magazine - Non-fiction: Stakes and chips Las Vegas and the internet have helped poker become the biggest game in town'. Financial Times. Retrieved 2010-01-10.
- ^Martain, Tim (2007-07-15). 'A little luck helps out'. Sunday Tasmanian. Retrieved 2010-01-10.

